Law of Large Numbers

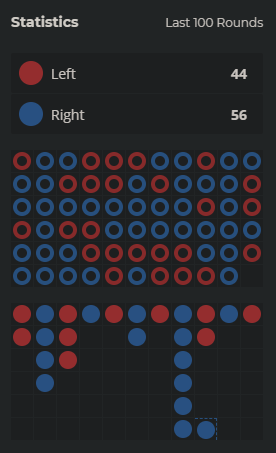
You probably would want to bet on Left, am I right?

This prediction of your behavior is made based on the law of large numbers. Even if you aren’t familiar with this law, you are most likely aware of it subconsciously, and you subconsciously apply this law to make all kinds of decisions and predictions in life.

What is the Law of Large Numbers?

The law of large numbers states that as the number of trials and their outcomes increases, the average of the results gets closer to the expected value. This law is important because it guarantees that the average of random outcomes will eventually be close to the number based on theoretical or expected probability if a large number of trials have been observed.

To give you an example, let’s consider a coinflip. We all know that the expected probability of flipping heads is 50%. This, however, does not guarantee that if you flip the coin 10 times, you will get 5 heads. You might only get 2 heads, or you could even get 10 heads, which is far from the expected probability. But if you flip the coin a million times, the results would most likely be close to 50%. If you flip the coin indefinitely, the cumulative results would be 50%, if not, extremely close to it.

Since the law pretty much guarantees that with a large enough number of trials, the overall average approaches the expected probability, it is often used in gambling, which leads to a common misconception.

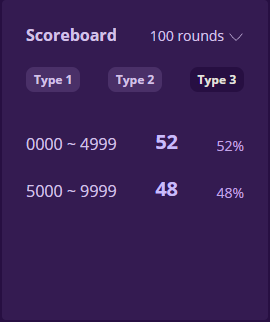
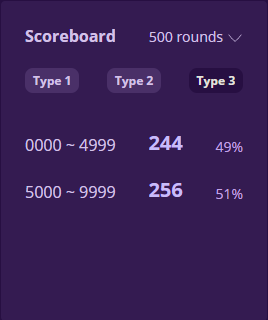
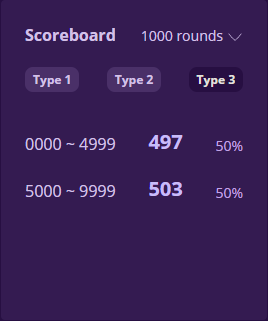
Gambler’s fallacy

This misconception, called gambler’s fallacy, refers to people’s tendency to believe that the next outcome will be affected by previous outcomes due to the law of large numbers.

If 10 coinflips resulted in 10 heads, you probably would bet the next flip to be tails, because you believe the proportion of heads to tails is supposed to even out to 50%. You are guessing what the next random outcome would be based on previous outcomes. However, it does not work this way, as each coin flip is an independent event, not affected by any of the previous events. So starting out with 10 heads does not mean you are more likely to get tails next. The law of large numbers simply means that those 10 heads will eventually be evened out with more tails at some point in a large number of flips, causing the proportion to become closer to 50%.

Applying the Law of Large Numbers in Peergame

In some ways, the law of large numbers can be used as a guide to navigating through randomness. Even though you can never be certain of what the next coin flip would result in, you can always be certain that over time, you will end up having about half heads and half tails. You can apply this principle to many different strategies to win more and lose less over time. At Peergame, we provide statistics for all games. Use this wisely to your advantage, and always remember to play responsibly. Good luck!